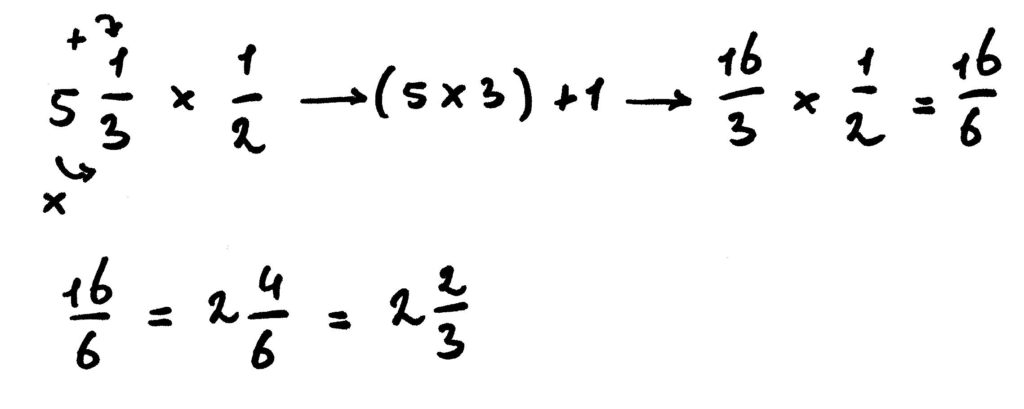Check of je het snapt!
Hieronder staan enkele oefenopgaven die je kunt oplossen met behulp van
de stelling van Pythagoras. Onderaan deze pagina staan de antwoorden
van de opgaven. Als het je niet lukt, kun je uitleg lezen als je op de
blauwe knop 'Informatie' klikt.
Opgave 1
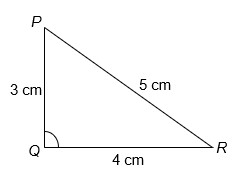
Gegeven is DPQR met PQ = 3 cm, QR = 4 cm en PQ = 5 cm.
Ga na of ∠Q = 90° door gebruik te maken van de stelling van Pythagoras.
Opgave 2
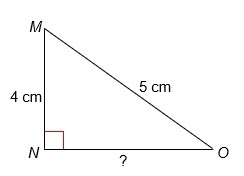
Gegeven is DMNO met MN = 4 cm, MO = 5 cm en ∠N = 90°.
Bereken de oppervlakte van deze driehoek in cm2. Oppervlakte
DMNO = ½ ⋅ NM ⋅ NO.
Opgave 3
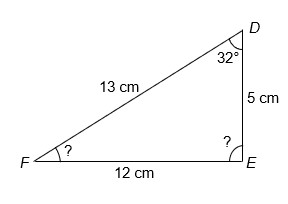
Gegeven is DDEF met ∠D = 32°, DE = 5 cm, EF = 12 cm en DF = 13 cm.
Bereken ∠F in graden.
Opgave 4
In een ruimte van 241 cm hoog ligt een kast van 60 cm bij 236 cm.
De diepte van de kast is niet belangrijk in deze opgave. Bereken met
de stelling van Pythagoras of je deze kast kunt kantelen in deze ruimte.
Opgave 5
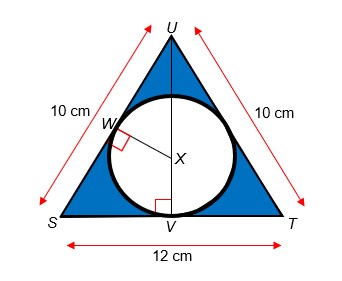
Gegeven is de gelijkbenige driehoek STU met ST = 12 cm en SU = TU = 10 cm. Loodrecht
op zijde ST ligt punt V met SV = VT en loodrecht op zijde SU ligt punt W. In
DSTU bevindt zich een cirkel met middelpunt X die de drie zijden van de
driehoek raakt. Er geldt WX = XV en 10 ⋅ WX = 36 − 4,5 ⋅ WX.
Bereken het oppervlak dat buiten de cirkel maar binnen DSTU ligt in
dm2 en rond af op twee decimalen. Oppervlakte cirkel = π ⋅
WX2. Oppervlakte DSTU = ½ ⋅ ST
⋅ UV.
Antwoorden
Probeer met de muis de antwoorden tevoorschijn te laten komen!
Opgave 1
Zie de schets hieronder.
De stelling van Pythagoras geldt alleen
in rechthoekige driehoeken, dus als ∠Q = 90°.
PQ2 + QR2 = PR2
(3 cm)2 + (4 cm)2 = (5 cm)2
9 cm2 + 16 cm2 = 25 cm2
De stelling van Pythagoras geldt in DPQR,
dus ∠Q = 90°.
Opgave 2
Zie de schets hieronder.
NO2 = MO2 − MN2
NO2 = (5 cm)2 − (4 cm)2
NO2 = 25 cm2 − 16 cm2 = 9 cm2
NO = √(9 cm2) = 3 cm
De oppervlakte van DMNO is ½ ⋅ MN ⋅ NO = ½ ⋅ 4 cm
⋅ 3 cm = 6 cm2.
Opgave 3
Zie de schets hieronder.
De stelling van Pythagoras geldt alleen
in rechthoekige driehoeken, dus als ∠E = 90°.
DE2 + EF2 = DF2
(5 cm)2 + (12 cm)2 = (13 cm)2
25 cm2 + 144 cm2 = 169 cm2
De stelling van Pythagoras geldt in deze driehoek, dus is ∠E = 90°.
Als je de drie hoeken in een driehoek bij elkaar optelt, kom je altijd uit
op 180°, dus
∠F = 180° − ∠D − ∠E = 180° − 32°
− 90° = 58°.
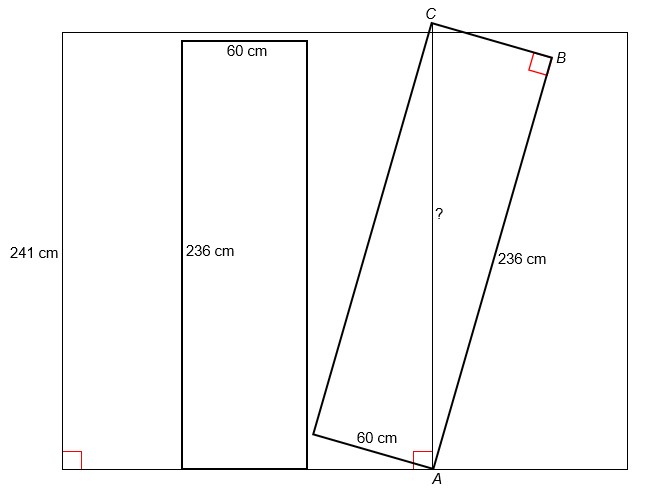
Opgave 4
Zie de schets hieronder.
Noem het punt van de kast rechtsonder A,
het punt rechtsboven B en het punt linksboven C. Als de kast
op zijn hoogste kantelpunt staat, staat de diagonaal AC loodrecht op
de grond. ∠B = 90°, dus geldt de stelling van Pythagoras in
DABC.
AB2 + BC2 = AC2
AC2 = (236 cm)2 + (60 cm)2
AC = √(55696 cm2 + 3600 cm2) ≈
243,5 cm
De kast kan dus niet gekanteld worden in een ruimte van
241 cm hoog.
Opgave 5
Zie de schets hieronder.
SV = ½ ⋅ ST = ½ ⋅ 12 cm = 6 cm.
In DSVU geldt de stelling van Pythagoras, want VU staat loodrecht
op ST, dus ∠V = 90°.
VU2 = SU2 −
SV2
VU2 = (10 cm)2 − (6 cm)2
VU2 = 100 cm2 − 36 cm2 =
64 cm2
VU = √(64 cm2) = 8 cm
De oppervlakte van DSTU is ½ ⋅ ST ⋅ VU = ½ ⋅
12 cm ⋅ 8 cm = 48 cm2.
Nu moet de straal van de cirkel (het
lijnstuk WX) worden berekend.
10 ⋅ WX = 3,6 − 4,5
⋅ WX
10 ⋅ WX + 4,5 ⋅ WX = 36
14,5 ⋅ WX = 36
WX = 36 cm ÷ 14,5 cm = 2,48... cm
De oppervlakte van de cirkel is
dus (2,48... cm)2 ⋅ π = 19,36... cm2.
Het oppervlak dat binnen DSTU maar buiten de cirkel ligt is dus
gelijk aan
48 cm2 − 19,36... cm2 = 28,63... cm2
≈ 0,29 dm2.